基于神经网络理论的水质评价模型的比较研究
基于神经网络理论的水质评价模型的比较研究
摘要:本文以MATLAB神经网络工具箱为平台,建立了BP-LM和LVQ两种地表水神经网络水质评价模型。研究结果表明,BP-LM网络的计算速度和收敛速度远高于LVQ网络,BP-LM网络模型比较适合于水质评价。本文也观察了大小样本对网络模型训练的影响,发现LVQ网络模型不适宜用大训练样本进行训练,而BP-LM网络对训练样本的大小不敏感,这有助于构建大容量有代表性的训练样本。
关键词:人工神经网络;BP-LM网络;LVQ网络;训练样本;水质评价
1前言
水是人类生存和发展的物质基础。随着生产的发展和人口的增长,水资源短缺、水质污染问题越来越突出。水环境质量评价是认识和研究水环境的一项重要内容,其目的是准确反映环境的质量和污染状况,预测未来的发展趋势,是水环境管理保护和治理的一项重要基础性工作。水环境质量评价是指通过对水体的一些物理、化学、生物指标的监测、调查,根据不同的目的和要求,按一定的方法对水体的质量做出估计。通过对水质进行评价,确定其污染类型,准确地指出水体当时的污染程度,为保护水体、水质提供方向性、原则性的方案和依据。
由于影响水质的因素很多,且因素与水质类别之间通常存在复杂的非线性关系,所以迄今没有一种统一的和公认的评价方法。目前应用于水质评价的方法发展了很多,大多是基于传统数学(统计学)、模糊数学和灰色数学的评价模型,如单项污染指数法、综合污染指数法、模糊综合评判法、灰色关联度分析法、灰色局势决策法、物元分析法等[1-2]。单项污染指数法只能评价水体中某种污染物的危害程度,不能反映水体中各种污染物的综合影响;综合污染指数法采用一个简单的数字指标作为硬性界限,忽视了这种分类或分级界限的模糊性;而基于模糊数学和灰色数学的综合评价方法,虽然注意到了这种实际上存在的分类或分级的模糊性,但在各水质污染物指标权重的选择上常带有主观性和随意性,因而存在一定的局限性。
人工神经网络(ArtificialNeuralNetwork,简称ANN)是起源于20世纪40年代,在80年代取得突破并迅速发展和广泛应用于众多学科的非线性模拟技术,是目前最活跃的前沿科学之一。ANN是对人脑神经元巨系统的生理特征和功能的抽象和模拟,具有自适应、自学习的特点,非常适合于研究和解决复杂的非线性问题。
从80年代末开始,我国的环境保护工作者开始将神经网络技术引入环境质量评价工作,建立了基于误差反向传播(BP)网络、霍普菲尔德(Hopfield)网络、径向基函数(RBF)网络、自组织特征映射(SOFM)网络、学习向量量化(LVQ)网络等数10多种评价模型,但其中80-90%是基于BP网络模型及其变化模型[2]。
本研究针对地表水环境质量评价,以MathWorks公司开发的MATLAB(R14SP1)神经网络工具箱(4.0.4版本)为平台,建立了基于Levenberg-Marquardt训练算法的BP网络的评价模型(BP-LM)和基于LVQ网络的评价模型(LVQ),分别用大训练样本和小训练样本进行训练,用检测样本评价训练效果及网络模型的性能,比较分析大、小训练样本对网络模型训练的影响以及两种模型的优劣。
2训练样本的准备
在神经网络模型的建立之中,训练样本占有非常重要的位置。在进行模式识别的过程中,主要依靠在训练之中获得的权重,这将直接影响数据的处理与最后的结果。在一般的神经网络进行实验中,采用的是小样本的方法,这使得整个模型在训练学习的过程简化了,也使得模型不能够得到足够多的数据来支持他的结论。神经网络又称为人工智能,主要是因为他可以在人为给定的数据中,自主的学习,寻找给定的数据之间的联系与关系,从而进行最后给定的数据的分类,如果人为给定的数据量很少,则整个网络无法得到有效的训练和学习,从而在最后判定数据的分类上存在一定的偏向性。
2.1地表水环境质量评价标准
实验的标准采用2002年6月1日实施的水质评价标准GB3838-2002的评价标准,采用了在标准中的DO、BOD5、石油类、挥发酚、氨氮、高锰酸钾指数,这6项指标作为评价项目。具体标准见表1。
表1地表水环境质量标准(GB3838-2002)单位(mg/L)
2.2检测样本
在实验的数据上,本实验选取参考文献[2]中的水质监测资料作为检验数据,见表2。
表2检验数据单位(mg/L)
2.3训练样本
采用小样本直接使用水质标准,其在二维平面内的投影分布见图1。
大样本采用MATLAB提供的RAND函数在各级评价标准内按随机均匀分布方式线形插生成训练样本,每级生成200个样本,共生成1000个训练样本。对应的目标输出理论值I级为1,II级为2,其他依此类推。其在二维平面内的投影分布见图2
对于BP-LM网络模型,其评价结果属于I级水质的输入,期望输出应为0~1之间的数值;对于评价结果属于II级水质的输入,期望输出应为1~2之间的数值;其他依此类推。
对于LVQ网络模型,其评价结果属于I级水质的输入,期望输出应为1;对于评价结果属于II级水质的输入,期望输出应为2;其他依此类推。
3BP-LM网络模型的建立及仿真结果
3.1BP-LM神经网络的原理与结构
3.1.1原理
BP网络,即多层前馈神经网络,因其采用误差反向误差传播算法(ErrorBackpropagation)而得名,1986年由D.E.Rumelhart等人提出。BP算法结构简单、易于实现。BP网络是一种分层型网络,由输入层、隐含层、输出层组成。层与层之间采用全互连方式,同一层的单元则相互不连接,输入层和输出层的单元数是由具体问题的输入层参数和输出层参数来确定的,而隐含层的单元数则由具体问题的复杂程度、误差下降情况等来确定。基本运行机制是:由信息正向传播和误差反向传播2个过程组成,工作原理详见文献[3-6]。
图3中所示的BP网络模型,输入为2维向量;1个隐含层,4个隐含神经元,传递函数为tansig;输出层3个神经元的结构,传递函数为purelin。
把输入模式映射到相应分类器所需知识由权值来体现。最初,被给定问题域的权值是未知的,直到找到有用权值之前,神经网络不能解决这个问题。寻找有用权值集合的过程,称为训练。在介绍网络模型的训练之前,引入一个概念:目标网络误差,即度量网络收敛到其期望值的程度的度量值。
训练步骤可归纳如下:
(1) 初始化,选定结构合理的网络,置所有可调参数(权重和偏量)为均匀分布的较小数值;
(2) 对每个输入样本作前向计算;
(3) 当数据处理达到目标网络误差时,训练完毕,反之则进行反向计算,即将输入样本再次输入和在前一次计算中得到修正的权重一起训练,再次修正权重。
这样,整个网络经过训练和学习而具有鉴别能力,在给定一个表示输入模式的由一系列特征组成的输入向量后,训练过的网络就可以作为强识别器来使用。
相对于其他的网络模型来比较,BP网络要成熟的多,但他的问题也相对比较突出,比如收敛速度慢以及存在所谓局部最小值的问题。这些可以通过Levenberg-Marquardt(简称LM)算法来解决。
设X(k)表示第k次迭代的权值和偏量所组成的向量,新的权值和偏量组成的向量XK+1可根据下面的规则求得:
XK+1=X(K)十△X(1)
对于牛顿法则是:
△X=-[▽2E(x)]-1-▽E(x)(2)
(2)式中▽2E(x)表示误差指标函数E(x)的Hessian矩阵;▽E(x)表示梯度。
设误差指标函数为:
E(X)=1/2ΣNi=1ei2(x)(3)
(3)式中e(x)为误差,那么:
▽E(x)=JT(x)e(x)(4)
▽2E(x)=JT(x)e(x)+S(x)(5)
在(4)、(5)式中S(x)=ΣNi=1ei(x)▽2ei(x)为Jacobian矩阵。
对于高斯-牛顿法的计算法则有:
△X=-[JT(x)JT(x)]-1JT(x)e(x)(6)
LM算法是一种改进的高斯-牛顿法,它的形式为:
△X=-[JT(x)JT(x)+μI]-1JT(x)e(x)(7)
从(7)式可看出,如果比例系数μ=0。则为高斯-牛顿法;如果μ取值很大,则LM算法接近梯度下降法。每迭代成功一步,则μ减小一些,这样在接近误差目标的时候,逐渐与高斯-牛顿法相似。高斯-牛顿法在接近误差的最小值的时候,计算速度更快,精度也更高。由于LM算法利用了近似的二阶导数信息,它比梯度下降法快
| 评论 |
|
|
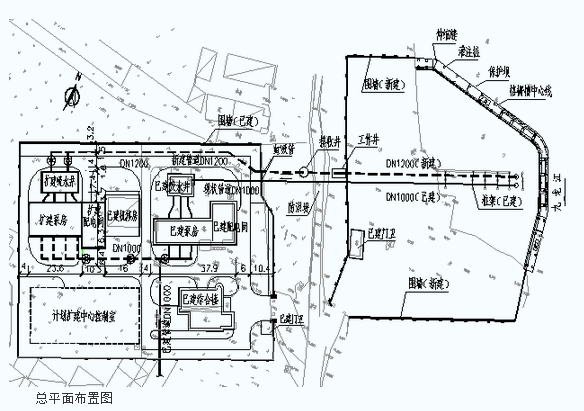 |
典型取水泵站扩建工程设计 |
| 论文导读:取水头部。设计采用新型双排拉森钢板桩围堰。虹吸管。穿越防洪堤。抽真空系统。总平面布置图.. |
热门文章
轻轻松松读懂地质报告
1、如何阅读勘察报告(1)直接看结束语和建议中的持力层土质、地基承载力特征值和地基类型以..[详细]